Archive
This post is archived and may contain outdated information. It has been set to 'noindex' and should stop showing up in search results.
This post is archived and may contain outdated information. It has been set to 'noindex' and should stop showing up in search results.
Fast Unit Vector Calculation for 2D Games
Jun 17, 2011ProgrammingComments (3)
Here's a quick description of a unit vector for those that don't know. A unit vector is a vector with a magnitude (distance) of 1. The vector can be pointing in any direction, but the magnitude will always be 1. To get a unit vector from any old vector, you "normalize" that vector, which gives you a new vector with the same direction but a magnitude of 1. Unit vector and normalized vector are often used interchangeably.
Take a look at this graph. Notice that while (1,0) is a unit vector, (1,1) is not. Think about the actual length of the line (it's magnitude) and you'll understand why (1,1) is not a unit vector.
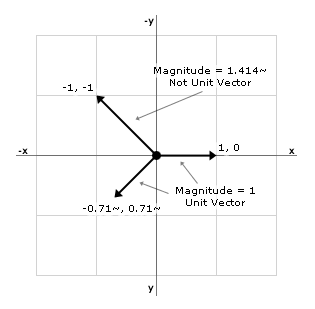
Note: Tilde (~) means approximate
To get a unit vector, the easiest and most accurate way is to divide each part of the vector by the vector's magnitude (length). Here is an example:
You can also use trigonometry to calculate it, but it is slower:
Both code blocks above will give you the same unit vector.
In 2D gaming, you often use unit vectors along with multipliers to calculate a projectile's vector based on the speed you want it to travel at. Take a look at this example:
The above will give you a vector from player to enemy that will travel 12 per iteration, regardless of the angle of the vector or how far away enemy was from player.
This is all fine and good, but the square root function and the two divisions can slow things down if you're using it a lot every frame (and the trigonometry version is slower yet). You probably don't need perfectly-accurate calculations for your game, so it is often better to use an approximation that is faster.
Here is an approximation that I came up with for the unit vector:
This is faster mainly because it doesn't use a square root function and only uses one division instead of 2. Ideally, I would like to get rid of the division, but I haven't figured out a way yet. Depending on your programming language, using conditionals in place of the abs and max functions will be faster.
I'll try to explain the ratio. What it does is look at the x and y parts of the vector, and adjust them from 100% to 70.711% based on how close their absolute values are to each other (how diagonal the vector is essentially). The inverse of the square root of 2 is roughly 0.70711, which is where I get the 0.29289 from (1 - 0.29289 = 0.70711).
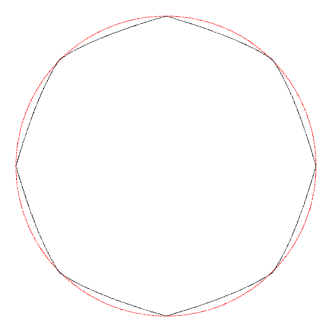
Visually, this is what the equation would create if you used it with a speed of 150 and fired projectiles in every direction. The red circle is a "perfect" circle created with the regular (slow) sqrt equation. The black "circle" is created with the approximation. It isn't perfect, but it is close enough and is much faster:
Here is an example in ActionScript 3 (Flash) of a function that returns a normalized and speed-adjusted vector. "M" is the speed, which I add to the end of the ratio. Notice that I used condition checks instead of absolute value and max functions. Doing this is much faster in ActionScript 3. I also found that simple if/else statements were a little bit faster than using the ternary (short-hand) checks.
(sX and sY refer to the starting position; eX and eY refer to the ending position)
It is good to instantiate the variables that your function will use outside of the function, otherwise you will be instantiating them every time the function runs and it will slow down the function considerably.
Here is an example in an ActionScript 3 custom class:
Take a look at this graph. Notice that while (1,0) is a unit vector, (1,1) is not. Think about the actual length of the line (it's magnitude) and you'll understand why (1,1) is not a unit vector.

Note: Tilde (~) means approximate
Basic Method (slow)
To get a unit vector, the easiest and most accurate way is to divide each part of the vector by the vector's magnitude (length). Here is an example:
// The vector
x = 15
y = 23
// Get vector magnitude
m = sqrt(x * x + y * y)
// Divide by magnitude
x = x / m
y = y / mYou can also use trigonometry to calculate it, but it is slower:
// The vector
x = 15
y = 23
// Get radians
r = atan2(x, y);
// Use sine and cosine on the radians
x = sin(r)
y = cos(r)Both code blocks above will give you the same unit vector.
In 2D gaming, you often use unit vectors along with multipliers to calculate a projectile's vector based on the speed you want it to travel at. Take a look at this example:
// Get the vector from player to enemy
x = enemy.x - player.x
y = enemy.y - player.y
// The speed you want the projectile to travel
s = 12
// Get vector magnitude
m = sqrt(x * x + y * y)
// Divide by magnitude and multiply by desired speed
x = x / m * s
y = y / m * sThe above will give you a vector from player to enemy that will travel 12 per iteration, regardless of the angle of the vector or how far away enemy was from player.
Faster Method
This is all fine and good, but the square root function and the two divisions can slow things down if you're using it a lot every frame (and the trigonometry version is slower yet). You probably don't need perfectly-accurate calculations for your game, so it is often better to use an approximation that is faster.
Here is an approximation that I came up with for the unit vector:
// The vector
x = 15
y = 23
// Get absolute value of each vector
ax = abs(x);
ay = abs(y);
// Create a ratio
ratio = 1 / max(ax, ay)
ratio = ratio * (1.29289 - (ax + ay) * ratio * 0.29289)
// Multiply by ratio
x = x * ratio
y = y * ratioThis is faster mainly because it doesn't use a square root function and only uses one division instead of 2. Ideally, I would like to get rid of the division, but I haven't figured out a way yet. Depending on your programming language, using conditionals in place of the abs and max functions will be faster.
I'll try to explain the ratio. What it does is look at the x and y parts of the vector, and adjust them from 100% to 70.711% based on how close their absolute values are to each other (how diagonal the vector is essentially). The inverse of the square root of 2 is roughly 0.70711, which is where I get the 0.29289 from (1 - 0.29289 = 0.70711).
Visually, this is what the equation would create if you used it with a speed of 150 and fired projectiles in every direction. The red circle is a "perfect" circle created with the regular (slow) sqrt equation. The black "circle" is created with the approximation. It isn't perfect, but it is close enough and is much faster:

Here is an example in ActionScript 3 (Flash) of a function that returns a normalized and speed-adjusted vector. "M" is the speed, which I add to the end of the ratio. Notice that I used condition checks instead of absolute value and max functions. Doing this is much faster in ActionScript 3. I also found that simple if/else statements were a little bit faster than using the ternary (short-hand) checks.
var vX:Number, vY:Number, aX:Number, aY:Number, ratio:Number;
function getvect(sX:Number, sY:Number, eX:Number, eY:Number, M:Number):Point
{
vX = eX - sX; vY = eY - sY;
if(vX < 0) aX = -vX; else aX = vX;
if(vY < 0) aY = -vY; else aY = vY;
if(aX > aY) ratio = 1 / aX; else ratio = 1 / aY;
ratio*= (1.29289 - (aX + aY) * ratio * 0.29289) * M;
return new Point(vX * ratio, vY * ratio);
}(sX and sY refer to the starting position; eX and eY refer to the ending position)
It is good to instantiate the variables that your function will use outside of the function, otherwise you will be instantiating them every time the function runs and it will slow down the function considerably.
Here is an example in an ActionScript 3 custom class:
package
{
import flash.geom.Point;
public class MyFunctions extends Object
{
private var vX:Number, vY:Number, aX:Number, aY:Number, ratio:Number;
public function MyFunctions():void
{
}
public function getvect(sX:Number, sY:Number, eX:Number, eY:Number, M:Number):Point
{
vX = eX - sX; vY = eY - sY;
if(vX < 0) aX = -vX; else aX = vX;
if(vY < 0) aY = -vY; else aY = vY;
if(aX > aY) ratio = 1 / aX; else ratio = 1 / aY;
ratio*= (1.29289 - (aX + aY) * ratio * 0.29289) * M;
return new Point(vX * ratio, vY * ratio);
}
}
}